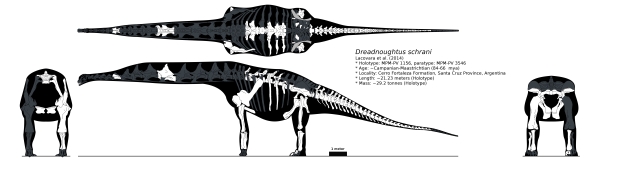
Dreadnoughtus was just described this past September by Lacovara et al. (2014). As per usual, both the paper and the media played up the size of Dreadnoughtus, with CNN in particular declaring on its website that it was “perhaps the biggest creature to ever walk the planet.” *Doublefacepalm* This should not be surprising for those who have followed science journalism covering paleontology, as nearly all gigantic sauropods that have been published in recent memory have had initial size estimates far higher than they likely were. For instance, “Seismosaurus”, Supersaurus, Argentinosaurus, Futalognksaurus, Puertasaurus – to name a few – were all declared to be the “biggest” at the time of their discovery but are now considered to be far smaller than initially reported. Only one of these, Argentinosaurus, may still be considered a contender for the biggest, although it too has had its size estimates reduced. Dreadnoughtus, however, is a particularly egregious example. In the paper, the mass was estimated at 59.3 tonnes, with the length estimated at 26 meters. However, doing my own skeletal reconstruction (see above) based on the 3D model in the supplementary material, I get a significantly different estimate.
My own mass estimate is about 29.2 tonnes, and the length estimate of 21.2 meters. In terms of mass, that is nearly a 50% difference! And the length estimate is still a difference of 18.5%. To get some perspective, that is like saying a person who is actually 5 ft 11 and 180 lbs is 7 ft tall and 360 lbs – a mighty big difference. Now, how did I get my estimate, and why is it so different? I got my estimate in a different way than the authors. I used a technique called Graphic Double Integration (GDI). I will go into detail this method and defend my reconstruction in future posts. For now, I want discuss my skepticism of the methods they used.
They used a mass regression model to predict the size based on methods in Campione & Evans (2012). Campione & Evans (2012) went to great lengths to rebut the slew of criticisms that have been made against these models in the past. Interestingly enough, the mass estimates they get for Giraffatitan and Diplodocus are quite close to mass estimates that I get using the GDI technique for both taxa. They estimate a mass of 26.8 tonnes – 44.7 tonnes for Giraffatitan, with a mean of 35.7 tonnes. A GDI estimate I did for Giraffatitan off of a figure by Greg Paul gave me an estimated mass of approximately 32.8 tonnes, which is quite close to the mean and right within the predicted range. Similarly, for Diplodocus I get a mass of about 10.5 tonnes, and they get a mean mass of 10.9 tonnes, with a range of 8.2 – 13.6 tonnes. Note that these mass ranges for both taxa are +/- ~25%. Applying the same range to Dreadnoughtus gives a range of 40.5 – 67.2 tonnes. The lower end of this range is closer to my estimate, but it is still off by about 25% – a significant difference.
So why is my estimate in this case so much lower than the equations used by Campione & Evans (2012)? One thing to note before I go on is that I think the similarity between my previous GDI estimates and how close they are to the regression method is possibly misleading. We are only working from a sample of 2, meaning the sample size is too small to draw any conclusions from this, it would be good to compare GDIs of the other taxa and compare them. For now, we are not able to do this. The real reason I suspect for this discrepancy is twofold: (1) the regression model is hit-and-miss when it comes to predicting masses in living taxa for which we already know the masses and (2) is that there is good reason to think that Dreadnoughtus is an outlier, and therefore would not be accurately predicted by the regression equation model.
How accurate are the regression equations when applied to living taxa?
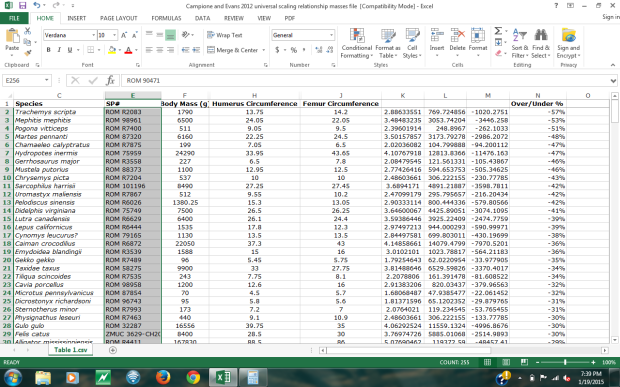
In regards to the first point, I took the 2nd regression equation from Campione and Evans (2012) and used it to predict the masses of the living taxa. Doing this, I found that for over a third of the taxa the predicted mean mass that was +/-30% or greater from the observed living mass of the taxa. This is a significant problem, because it shows that for a significant portion of living taxa, the regression model produces a poor fit when predicting masses. In addition, 35 of the 255 taxa had predicted mean masses that were +/-50% from the observed mass, which is nearly 1 in 7 taxa. From this data, it should be clear that while the majority of the taxa have reasonable mass predictions, enough fall out of a range that I would consider reasonable to suggest that, used alone, the regression equations may not be sufficiently robust to predict masses of extinct animals. At the very least, another independent method should be used to give a check on mass estimates. I would suggest that a relatively easy method to do this would be GDI techniques. 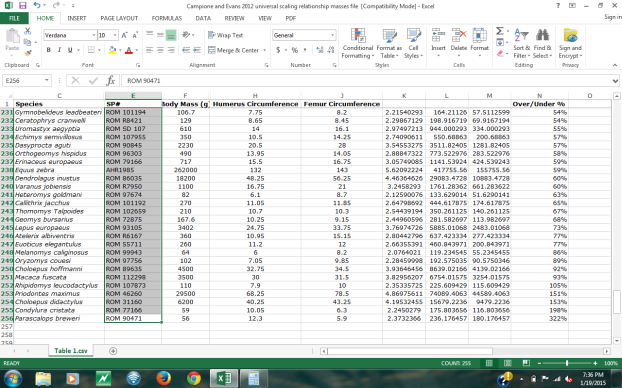
Is Dreadnoughtus an outlier?
In regards to the second point, I suspect Dreadnoughtus may be an outlier (being in the range of masses of by more than +/- 50%) because the referred limb bones of Futalognkosaurus are very similar in size to Dreadnoughtus in terms of length. While femur length is a poor indicator of overall size and mass, in other comparable measurements (cervical vertebra size, pelvis size, etc.), it appears that Futalognkosaurus is quite similar in size in general to Dreadnoughtus. Futalognkosaurus was found by Benson et al. (2014) to have a mass of about 38.1 tonnes, which is not too different than my GDI estimate for Dreadnoughtus (although it should be noted that my GDI mass estimate for Futalognkosaurus is considerably lower than these estimates – that said, I consider my Futalognkosaurus reconstruction to be out of date in a number ways). Another reason why Dreadnoughtus is probably an outlier, and therefore not predicted well by the regression equations, is that in statistics there is the danger of extrapolation. This refers to using statistical models to predict values out of the range of the sample data. In this case, while Campione & Evans (2012) do an admirable job of trying to rebut criticism of this, I don’t think they do a very effective job.
For instance, in their data set the largest animal they have data for is Loxodonta africana, at about 6.4 tonnes. This is in comparison to masses of many sauropods which easily out classing this, as even the rather light Diplodocus is at least 50% heavier than this. The predicted mass of Giraffatitan being over 450% heavier than the heaviest taxon in the sample. Therefore, there is good reason to be skeptical of extrapolating animals much larger than the sample the regression equations are based on.
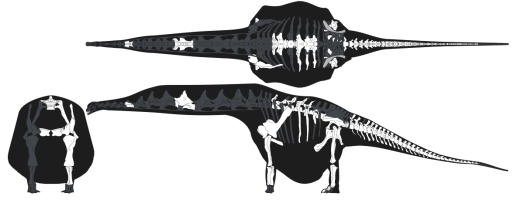
For fun, here is what a 52 tonne Dreadnoughtus looks like with the soft-tissues of my skeletal increased by 50% on the torso and 25% on the neck:
And here is a screen shot of the calculation:
 Me thinks that is not very likely.
Me thinks that is not very likely.
Up next: A GDI mass estimate for Dreadnoughtus.
References:
Benson, R. B. J., Campione, N. E., Carrano, M. T., Mannion, P. D., Sullivan, C., Upchurch, P. & Evans, D. C. Rates of dinosaur body mass evolution indicate 170 million years of sustained ecological innovation on the avian stem lineage. PLoS Biol. 12, e1001853 (2014).
Campione, N. E. & Evans, D. C. A universal scaling relationship between body mass and proximal limb bone dimensions in quadrupedal terrestrial tetrapods. BMC Biol. 10, 1–22 (2012).
Lacovara, K.J. et al. A Gigantic, Exceptionally Complete Titanosaurian Sauropod Dinosaur from Southern Patagonia, Argentina. Sci. Rep. 4, 6196; DOI:10.1038/srep06196 (2014).